首先先说一下最后一个测试点很多人RE的问题,我来了一张图:

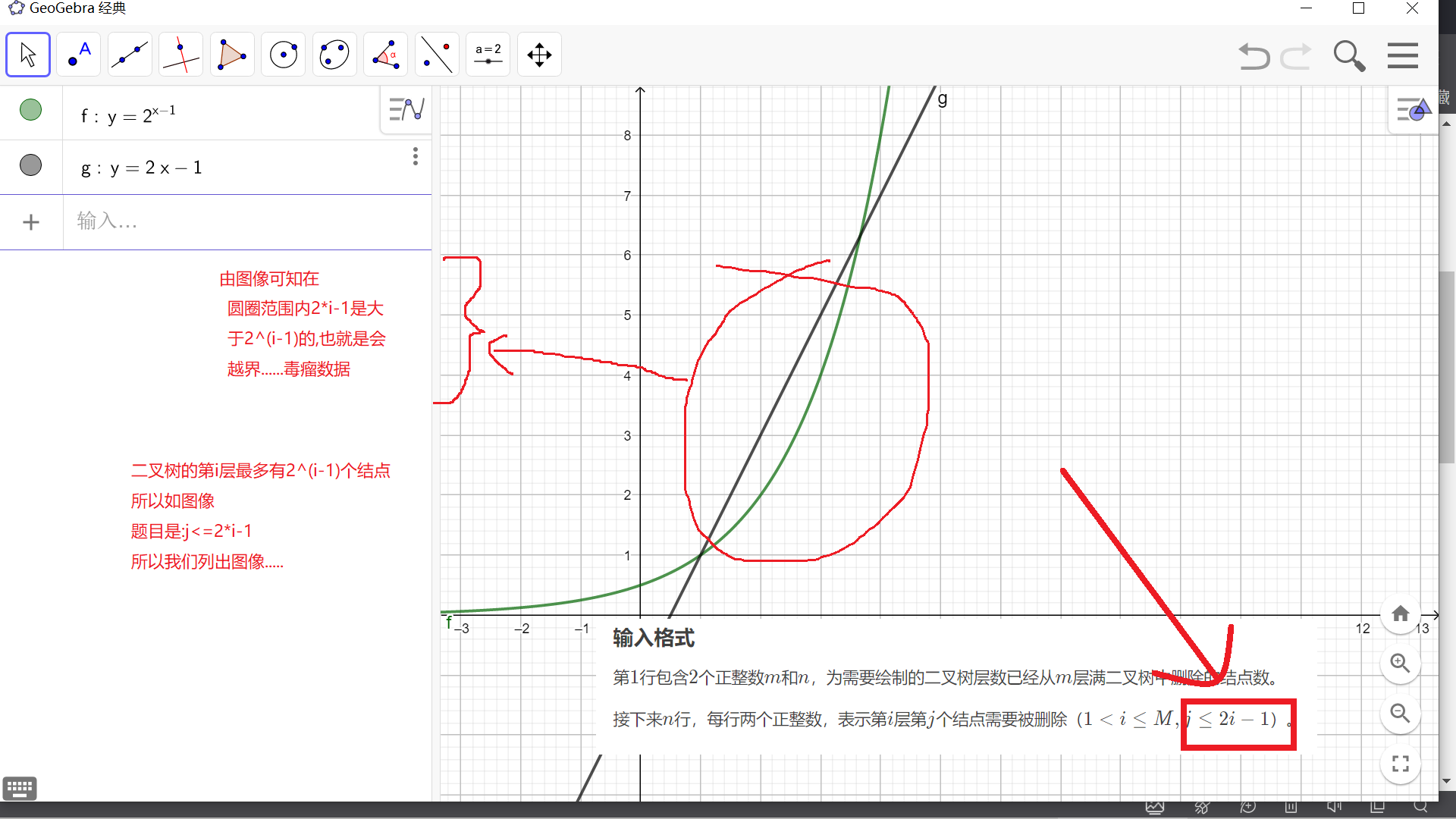
大概就是图里的那样…

下面是我的思路:
可能稍微复杂一点…

首先,题意我就不说了,关键在于每一层的边长度不同:
大佬们已经推出来这么个东西:

1
f[20]={0,1,2,5,11,23,47,95,191,383,767};

其中f[i]就是高度为i的那一层到它上一层的边的长度(这里的高度指的是由下往上数的高度,为了方便我把最下边设为了1)
举个例子(样例):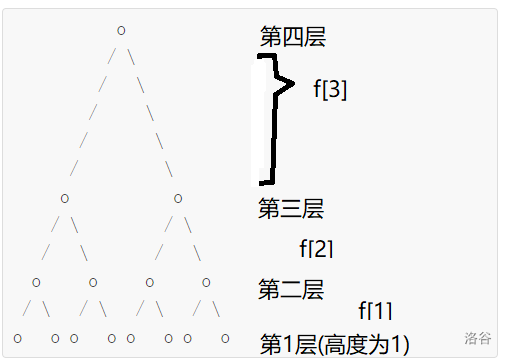
也就是说f[i]存的就是第i层到第i-1层的边的长度(几个’/‘或’\’)

我是先把最下边一层先初始化弄进去,因为我不知道n,所以我从我开的画布数组最下边一行开始,从下往上:

1
2
3
4
5
6
7
cin>>n>>k;
num=1<<(n-1);
for(long long i=1,j=1;i<=num/2;++i,j+=6)
{
		paint[19000][j]='o';
		paint[19000][j+4]='o';
}

两个一组,很容易得出最下面一行共需要(2^(n-1))/2次循环,每次直接两个都放进去’o’,然后很容易的j每次加6(横坐标)

然后从倒数第二行开始模拟往画布里填’o’或’/‘或’\’
我们可以这样:计算出当前行的最左/最右结点在画布里的坐标为循环边界,从左边(当前行的所有结点视为向上一行的结点的孩子),即左孩子开始,向右上方朝父节点画’/’.

但是要画几次呢?这时我们的f[]数组就派上用场了…从第i层向上画’/'当然画f[i]次了,然后画完边后再向右上一格把父节点也就是’o’画上,然后从父结点再往右下画回到右孩子,然后这一个子树画完再画旁边的树,画个流程图吧: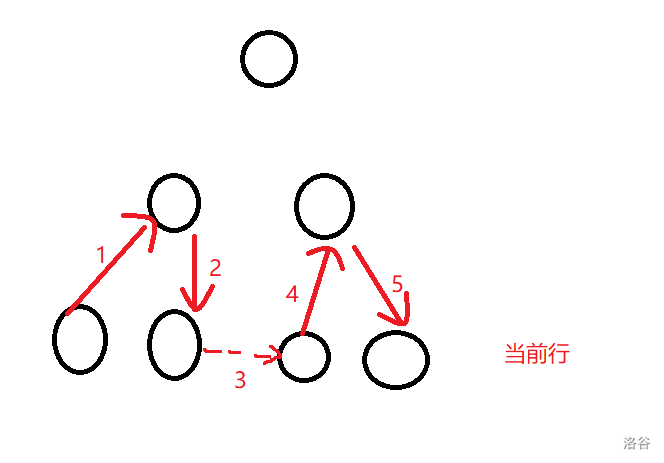

就是这样,先上去,再下来,然后虚线跳到下一个子树,注意这时跳跃的长度每层是不一样的,我们用s[]来存,很容易得出(跟f[]很类似):

1
s[20]={0,2,6,12,24,48,96,192,384,768,1536};

每次横坐标加就行了

这样,我们最后就有了一个完全二叉树,然后就是去节点了.
画布里存得是点或边在这张"画"里得坐标,而题目输入进来得是结点在树中得坐标,这时我们就开一个结构体数组存树,数组的每个元素为结点,每个元素(都是一个结构体变量)里的结构体成员x和y存的是通过计算求得的在画布里的坐标,然后找到要删除的点,把它和它的子树所在的一个正方形区都归为’ '(空格),如图: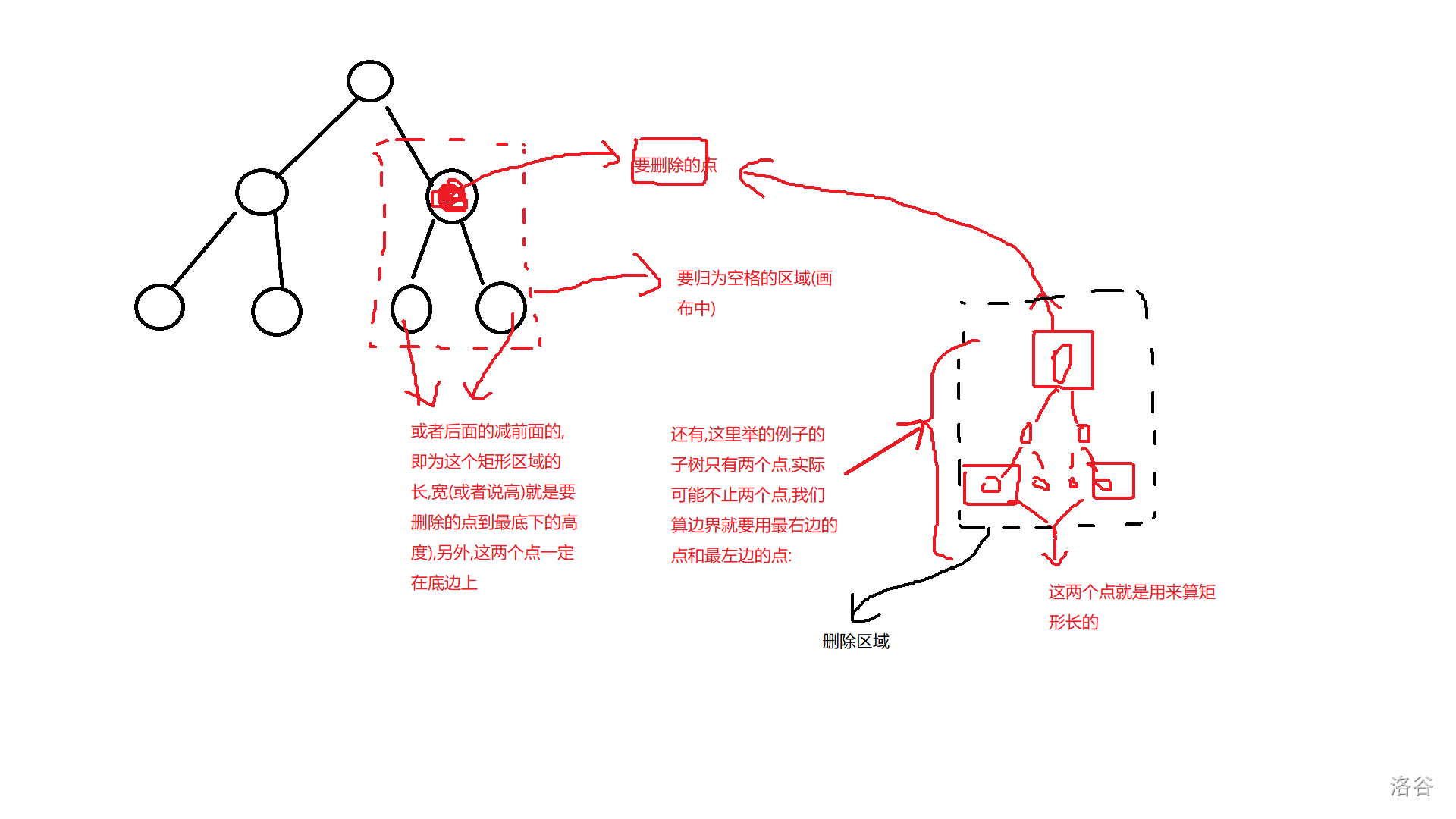

然后,愉快的输出就行了,其他的细节在代码中:

AC代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include<bits/stdc++.h>
using namespace std;
long long n,k,num,x,y,line=19000;
long long l,r,f[20]={0,1,2,5,11,23,47,95,191,383,767};//解释过了
long long s[20]={0,2,6,12,24,48,96,192,384,768,1536};//跳跃的长度
char paint[20001][5000];//画布
struct TREE
{
	long long x,y;
}tree[1040];
void draw(long long i)//画边和点
{
	x=line,y=l;
	l=y+f[i]+1;//l---左边界的重新计算要在这里
	for(long long j=1;j<=num/2;++j)
	{
		/////////向右上画//////////////
		for(long long k=1;k<=f[i];++k)
			paint[--x][++y]='/';
		paint[--x][++y]='o';
		//////////////////////////////
		/////////向右下画回去//////////
		for(long long k=1;k<=f[i];++k)
			paint[++x][++y]='\\';
		//////////////////////////////
		++x;
		y++;
		y+=s[i];
		//重新计算坐标
	}
	y-=s[i];
	r=y-f[i]-1;
	line=x-f[i]-1;
	num/=2;
	//把num---即当前行的结点数、
	//r---右边界、
	//line---最高点的所在行
	//重新计算为向上一行(左边界在上边重新计算)
}
void remove_down_all(long long up,long long r_l,long long r_r)//重置矩形区域
{
	for(long long i=up;i<=19000;++i)
		for(long long j=r_l;j<=r_r;++j)
			paint[i][j]=' ';
}
void remove_up_edge(long long x,long long y)//删除(重置为' '(即空格))要删除点向上与父亲的连线
{
	long long ex=x-1,ey=y-1;
	if(paint[ex][ey]!=' ')
		while(paint[ex][ey]!='o')
			paint[ex--][ey--]=' ';
	ex=x-1,ey=y+1;
	if(paint[ex][ey]!=' ')
		while(paint[ex][ey]!='o')
			paint[ex--][ey++]=' ';
}
int main()
{
	cin>>n>>k;
	if(n==0)
	{
		cout<<endl;
		return 0;
	}
	memset(paint,' ',sizeof(paint));
	num=1<<(n-1);
	long long num2=num;
	long long len=0;
	long long to=(num2/2)*6-1;//to为整棵树的宽度,我们要用它输出树(列循环范围)
	l=1;r=(num/2)*6-1;//初始化左右边界
	for(long long i=1,j=1;i<=num/2;++i,j+=6)//初始化最下面一行
	{
		paint[19000][j]='o';
		paint[19000][j+4]='o';
	}
	for(long long i=1;i<n;++i)//开始从下往上每一层"绘画"
		draw(i);

	for(long long i=line;i<=19000;++i)//计算坐标,用以删除结点
		for(long long j=1;j<=to;++j)
		{
			if(paint[i][j]=='o')
			{
				tree[++len].x=i;
				tree[len].y=j;
			}
		}
	long long t,y1,y2;
	for(long long i=1;i<=k;++i)//删除结点(每次删除之前的准备工作)
	{
		scanf("%d%d",&x,&y);
		t=1<<(x-1);
		t=t+y-1;
		if(t>len)continue;
		x=tree[t].x;
		y=tree[t].y;
		y1=y-(19000-x);
		y2=y+(19000-x);

		remove_down_all(x,y1,y2);
		remove_up_edge(x,y);//这两个函数才是真正的删除
	}
	//处理完了......
	for(long long i=line;i<=19000;++i)//输出,结束
	{	
		for(long long j=1;j<=to;++j)
			cout<<paint[i][j];
		cout<<endl;
	}
}

管理员求过…真的是自己的做法