提要:

  1. 本部分讲解C函数与数组的相关问题
  2. 并且引入递归的思想

前置知识:

  1. 充分掌握前面关于数组的知识
  2. 可能的话了解一点指针的概念

函数的递归

两种基本的思想

我们在求解各种问题的时候,往往会有各种方法,不过大部分方法分析起来,往往能归为几种基本的思想.常见的两种思想就是迭代和递归.

递归,是一种问题求解的思想,往往将一个问题转化为(若干个)规模更小的子问题进行求解.子问题逐渐细分到最小,此时就变得很容易求解.放到实际编程中来说,就是函数自己调用自己的过程.

另一种思想是迭代,简单来说,就是重复某一个过程,逐渐更新状态,一步步接近最终的结果,达到求解的效果放到编程语言中,一般是使用若干个,可以嵌套的循环 进行不断地重复逼近.

两种思想,仅仅是思想,并不代表具体的问题只能以某一种思路去求解,例如斐波那契数列的求解,就可以使用两种方法去写,下面也使用这个例子进行讲解.

什么是函数递归调用

递归是这样一种思想,侧重点为:将一个规模较大的问题分解为规模更小的子问题去求解,直到子问题足够小变得很容易计算,再依次返回并逐层完成依赖于这个子问题的更大规模的子问题,最终实现求解原本规模的问题.

实际上这种思想在数学中已经有所体现,例如函数:

f(x)={0x<=0f(x−1)∗3x>0f(x)=\left\{\begin{aligned} 0 \quad x<=0 \\ f(x-1)*3 \quad x>0 \\ \end{aligned}\right.

当x>0时,想要求出函数值,自然需要不断对x减1,才能得到最终的值,当然,这个简单的函数可以推导公式,但是这里的重点是递归.


我们举一个很简单的例子,那就是斐波那契数列,其数学公式为:

F(n)={0if n=01if n=1F(n−1)+F(n−2)if n>1F(n) = \begin{cases} 0 & \text{if } n = 0 \\ 1 & \text{if } n = 1 \\ F(n-1) + F(n-2) & \text{if } n > 1 \end{cases}

显然,我们也可以使用递推(数学上)的方式去进行逐个求解(相信各位都会手算).那么我们的问题是:如何使用C语言去实现这个递推的过程?


C语言的函数支持递归,也就是函数的自调用,那么根据递推公式,我们可以写下如下代码来计算斐波那契数列的第n个数:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <stdio.h>

int fibonacci(int n) {
    if (n <= 2) {
        return 1;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

int main() {
    int n;
    printf("请输入要计算的斐波那契数列的项数：");
    scanf("%d", &n);

    if (n <= 0) {
        printf("无效的输入\n");
    } else {
        int result = fibonacci(n);
        printf("斐波那契数列的第 %d 项是 %d\n", n, result);
    }
    return 0;
}

读者可以自行运行尝试.


代码解释:

在上面的代码中,我们在main函数中使用fibonacci(n)来计算第n项的值.关键在fibonacci()的代码中,我们可以看到,在函数的一开头,有一个判断,检查n的值是否为1或2(因为小于等于0的情况被main函数中的if给处理掉了).

如果n为1或2,显然,斐波那契数列的前两项都是1.那么该函数直接返回1作为结果即可(注意,我们此时丝毫不关心他返回到哪个函数!).

否则,n就是3及3以上的数,那么根据递推公式F[n]=F[n-1]+F[n-2],n>=3可知,我们需要分别计算fibonacci(n-1)和fibonacci(n-2),并把他们相加的值返回,也就有了return fibonacci(n - 1) + fibonacci(n - 2);这一条语句.

显然,这两个调用仍然是fibonacci()这个函数,只不过调用时使用的值不同而已.我们发现,每次在fibonacci()中调用自己,传递的参数不是n-1就是n-2,这样就保证最终在某一层的调用中,n的值减少到了1或者2,此时函数直接返回,不再需要进一步的递归.

到了这步,函数便逐层地结束,一层层地将运算的值返回给上一层,由上一层将这层的两次调用函数的返回值相加,把结果返回给再上一层,直到最终返回到顶层,即原来要求解的n.

最终,所有的递归调用的运算结果都汇总到一个fibonacci()的调用,也就是main()函数一开始调用的那一个,然后其再次返回相加的值(当然,如果n一开始就是1或者2,则根本不会有这么多的递归过程),赋值给main中的result变量.


运行结果:

image-20231108204235065

斐波那契的递归求解就是如此简单,只需要短短的3行即可.


我们使用CLion在return 1;下断点进行调试也能发现,函数逐层递归,直到最底层的(逻辑上的底层,实际的栈顶)一次调用结束,才能返回到上一层继续运行:

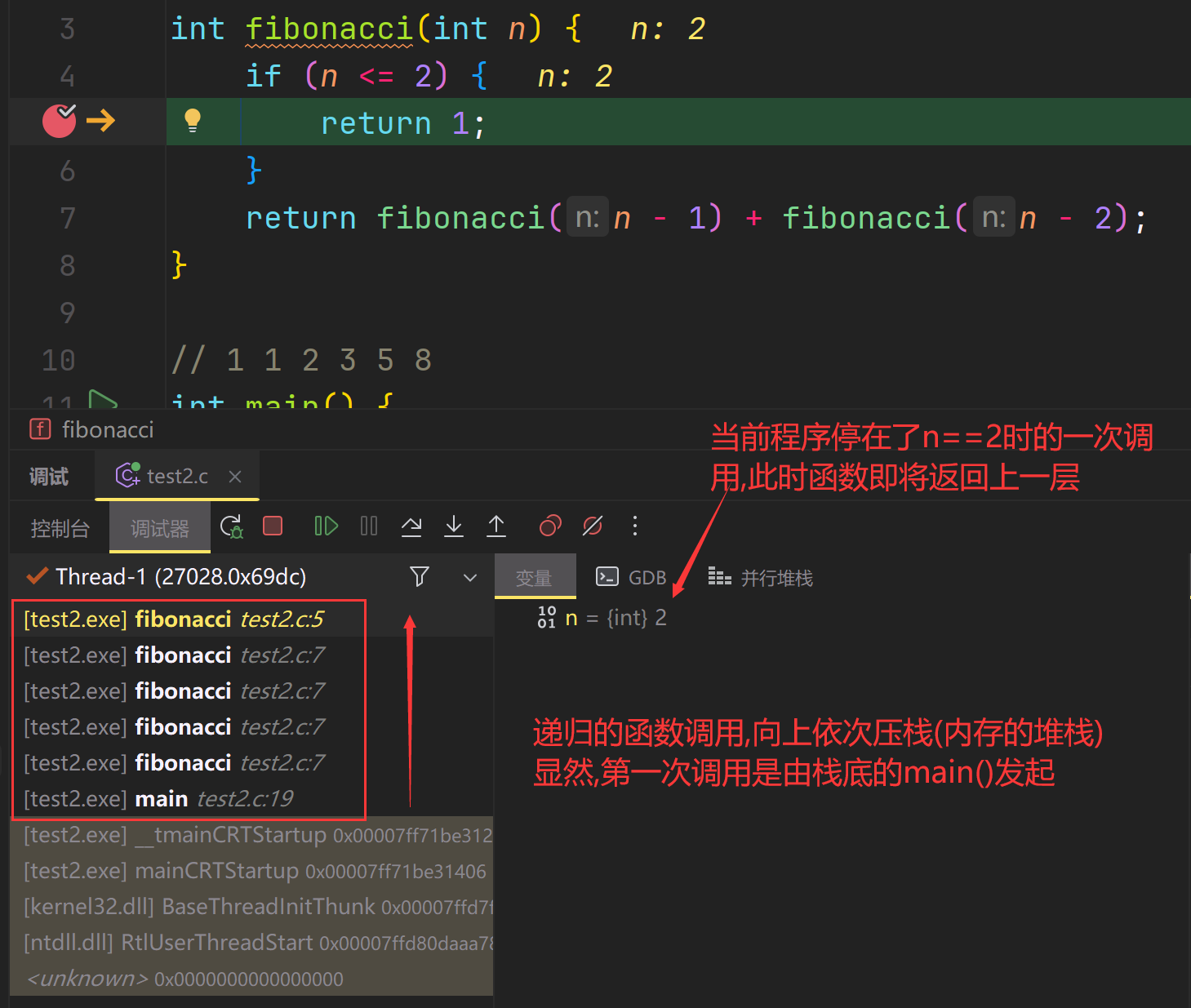
image-20231108204119666

当n为5时,实际上的调用过程类似这样:

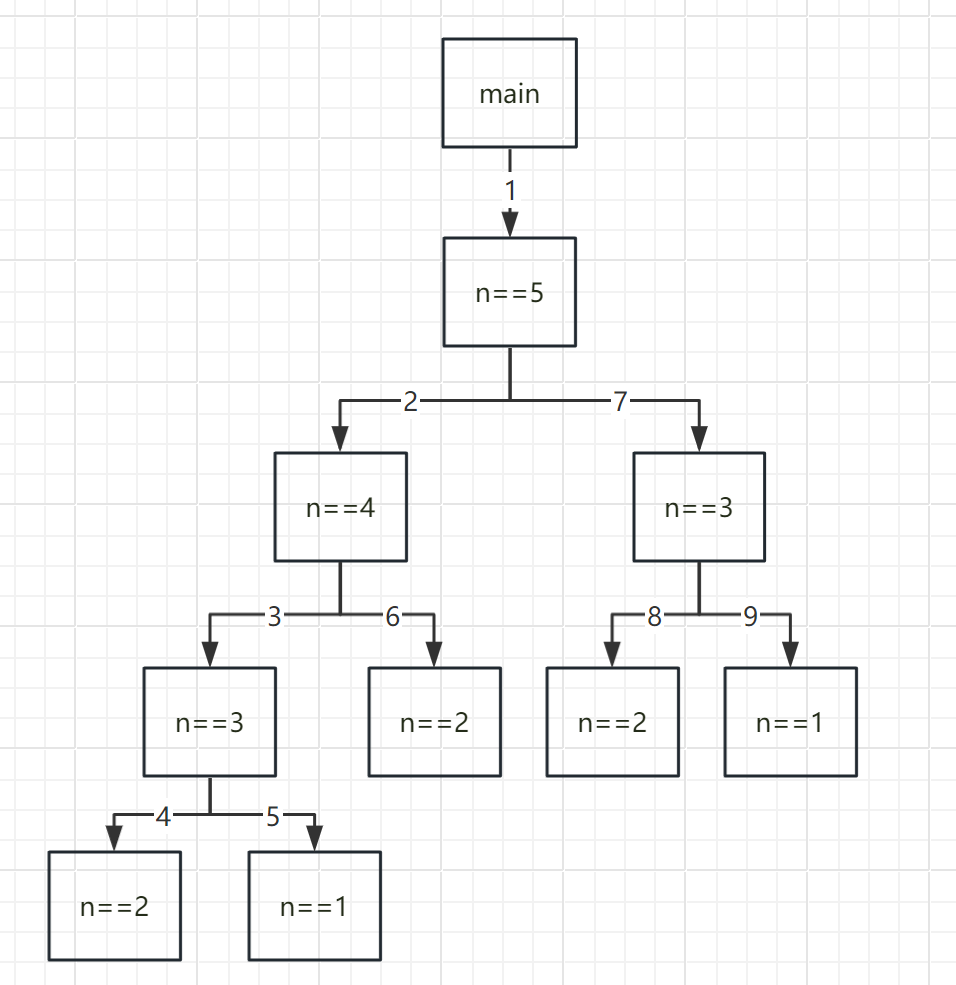
image-20231205172718566

其中箭头上的数字代表函数调用的顺序,例如第一个调用就是main()调用fibonacci(),此时n为5.

可以看到,return语句的表达式中有2个递归调用,所以调用链看起来就像是一个二叉树一样.

C函数与数组

可以数组作为参数?

先上结论

这是一个新手非常容易犯错的问题.十分明确的一点是,C语言中无论是函数参数还是函数返回值,都只能对应一个一般的变量,而不能将一个数组作为一个整体进行参数传递.

尽管我们某种程度上认为数组是"一个"变量(在后面讲解指针和数组的关系时会详细描述)—只不过被划分为各个子元素.但是C语言并没有提供一种方法,用以实现将整个数组作为参数进行传递,或者是将一个数组作为返回值进行返回.

而这一点看起来十分冲突,特别是在我们后面学习了结构体后这一问题会尤为突出.一种理解方式是,结构体的各个字段并不是单一的变量,而是作为结构体的一部分,一个结构体变量此时作为一个整体被视为一个单一的变量.

使用数组作为形参

尽管我们不能将一整个数组作为参数复制过去,但是我们仍然可以为函数制定一个数组形式的参数,但是这个参数很特殊.

我们看一个代码,这个程序用于输出某个数组的所有元素:

1
2
3
4
5
6
7
8
9
10
11
12
13
#include <stdio.h>

void print_arr(int arr2[10]) {
    for (int i = 0; i < 10; ++i) {
        printf("%d ", arr2[i]);
    }
}

int main() {
    int arr[10] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
    print_arr(arr);
    return 0;
}

运行结果:

image-20231111143707285

上面这个程序读起来十分容易,看上去print_arr()接受了一个"数组参数",然后将每一个元素进行输出.


但是下面的代码就会让你发现,对函数形参arr2的"各个元素"进行修改是会影响到main中的arr的:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <stdio.h>

void print_arr(int arr2[10]) {
    printf("change arr2 in print_arr\n");
    for (int i = 0; i < 10; ++i) {
        arr2[i] *= 2;
    }
    printf("arr2 in print_arr:\n");
    for (int i = 0; i < 10; ++i) {
        printf("%d ", arr2[i]);
    }
    printf("\n");
}

int main() {
    int arr[10] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
    printf("arr in main:\n");
    for (int i = 0; i < 10; ++i) {
        printf("%d ", arr[i]);
    }
    putchar('\n');
    printf("call print_arr():\n");
    print_arr(arr);
    printf("after call print_arr(),arr in main:\n");
    for (int i = 0; i < 10; ++i) {
        printf("%d ", arr[i]);
    }
    return 0;
}

运行结果:

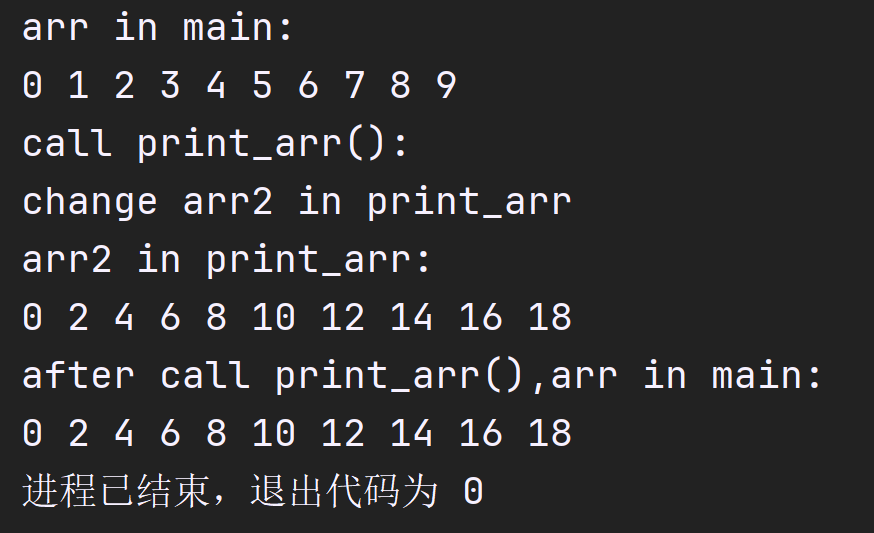
image-20231111151641994

显然我们可以看到main()函数中的arr数组也受到了影响.


上面的例子中可以看出,数组作为函数形参,并不会为整个数组生成一个副本(如果不理解请回看函数参数的按值传递),而是会以某种方式将实参"映射"过来,这就意味着在print_arr()中对形参arr各元素的修改,实际上修改的是main()函数中的数组arr的各元素.

事实上,print_arr()中根本就没有一个新的数组,仅仅是存在一个指向arr数组首元素的指针,这个指针就是arr2!

这里简单地抛出这个重要区别,读者一定注意!这和一般的参数不同.


想要解释这个问题,需要后续学习指针后才能进行讨论,这里可以记住:对于函数形参而言,传递数组就是在传递指针,而不是复制整个数组.

数组的长度信息

还有一个重要的事情,我们知道利用sizeof()可以计算数组的大小:

1
2
3
4
5
6
7
8
#include <stdio.h>

int main() {
    int arr[10] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
    int len = sizeof(arr)/sizeof(arr[0]);
    printf("%d",len); // 输出 10
    return 0;
}

即sizeof(arr)计算出arr数组的总长度(字节数),然后除以arr每一个元素的长度sizeof(arr[0]),就算出了数组的大小(元素个数)len.


但是放到函数参数这里就不再成立:

1
2
3
4
5
6
7
8
9
10
11
12
13
#include <stdio.h>

int get_arr_len(int arr2[10]) {
    int len = sizeof(arr2) / sizeof(arr2[0]);
    return len;
}

int main() {
    int arr[10] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
    int len = get_arr_len(arr);
    printf("%d", len); // 运行结果是错误的 2
    return 0;
}

原因很简单,函数形参arr2实际上是一个指针,而不是数组.

x64(我的环境是64位)的指针变量(int*)占用8个字节,而每一个元素(int)占用4个字节,两者相除结果就是2.

这就导致结果是错误的,所以,我们在对一个函数传递一个数组时,需要手动使用另外一个变量去传递数组的长度.

另一方面,尽管我们写了int arr2[10],但是这里的10被直接无视(实际上其可以被省略).原因一样,arr2只是一个指针.


我们要写一个函数输出一个数组的所有元素,但事先不知道其长度,可以这样:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <stdio.h>

// 如上所述,这里直接将10省略掉,使用另外一个形参len手动指定
void print_arr(int arr2[],int len) {
    for (int i = 0; i < len; ++i) {
        printf("%d ", arr2[i]);
    }
}

int main() {
    int arr[10] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
    print_arr(arr,10);
    return 0;
}

运行结果:

image-20231111153149707

可以返回一个数组?

和数组形参同理,返回值也是不可能返回一个完整的数组副本的.同样,如果写return arr2;,返回的将是一个指针.

而且提前告知一句:返回一个指针的函数,一定要确保指针不为NULL,或者没有指向某些意想不到的地方,例如该函数的某个局部变量,在函数返回后这个局部变量就被销毁了!

指针,指针与数组的关系比较复杂,会在后面进行讲解.

C99-变长数组形式参数

变长数组(VLA)

前面讲解数组时提到,数组变量的长度必须使用常量表达式给出,而在新标准C99中(其实已经不新,写这篇文章时已经更新到C23),也可以使用非常量表达式.这样的数组叫做变长数组(VLA).

我们使用变长数组可以自定义数组的长度,而不是必须进行动态内存分配.

下面是一个例子,用于存储并输出1~n:

1
2
3
4
5
6
7
8
9
10
11
12
13
#include <stdio.h>

int main() {
    // 存储并输出1~n
    int n;
    scanf("%d", &n);
    int arr[n];
    for (int i = 0; i < n; ++i) {
        arr[i] = i + 1;
        printf("%d ", arr[i]);
    }
    return 0;
}

变长数组函数形参

C99同时增加了几个与数组型参数相关的特性.

VLA作为函数形参,往往用于传递高维数组,因为高维数组必须确定第1维之后的各维的长度.

我们在传递二维数组形参时,可以这样:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <stdio.h>
// 第二维不可省略!,第一维,即需要输出几行,显式地使用另外一个参数给出
int print_arr2d(int arr[][4],int row){
    for(int i=0;i<row;i++){
        for(int j=0;j<4;j++){
            printf("%d ",arr[i][j]);
        }
        printf("\n");
    }
}

int main() {
    int arr[3][4]={
        {1,2,3,4},
        {5,6,7,8},
        {9,10,11,12}
    };
    print_arr2d(arr,3); // 输出这个二维数组
    return 0;
}

但是一旦main()中的数组列数发生变化,例如变成了5,程序就会发生错误.

C99的变长数组函数形参解决了这个问题,我们可以这样写:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>

// row和col两个参数必须在arr之前给出
int print_arr2d(int row, int col, int arr[row][col]) {
    for (int i = 0; i < row; i++) {
        for (int j = 0; j < col; j++) {
            printf("%d ", arr[i][j]);
        }
        printf("\n");
    }
}

int main() {
    int arr[3][4] = {
            {1, 2,  3,  4},
            {5, 6,  7,  8},
            {9, 10, 11, 12}
    };
    print_arr2d(3, 4, arr); // 这样写的话,print_arr2d()函数即可适用于任何大小的二维数组
    return 0;
}

本部分讲解了初学者能遇到的大部分函数问题,不过二维数组参数仍然没有讲解清楚,我会将相关的所有内容放到指针这一大篇章.

---WAHAHA



上一篇:C语言教程-12_2-深入分析函数和面向过程初识

下一篇:C语言教程-13_1-初识指针