概述

字符串匹配算法需要维护2个指针,分别为指向主串的i和指向模式串的j.
设主串的长度为n, 模式串的长度为m.

暴力匹配低效的原因

单纯的暴力匹配需要对指针进行回溯:

  • 对于主串的指针i, 从某一个起始点k开始匹配, 如果匹配失败则从k+1处重头开始匹配
  • 对于子串的指针j, 一旦上一次匹配失败, 那么这一次重新的匹配就需要重新归零, 即从模式串的开始重头开始匹配
    这样的回溯导致暴力匹配的时间复杂度为O(n*m), 非常低效.

KMP尝试改进的思路

与暴力相比, KMP试图尝试利用已经搜索过的主串信息. 先不管模式串, 因为模式串是固定的, 对于主串, 我们至少要将整个主串扫描一遍, 这需要O(n), 然而暴力方法在回溯i的过程中, 有着大量的字符被不止一次地重复扫描, 这是其效率低下的一个重要原因; 而另一个原因是, 每次重新匹配都需要让j归零, 但实际上很多情况下, 前面的部分根本不需要重新匹配, 因为扫描过的主串靠后面的位置很有可能与模式串前面相同.

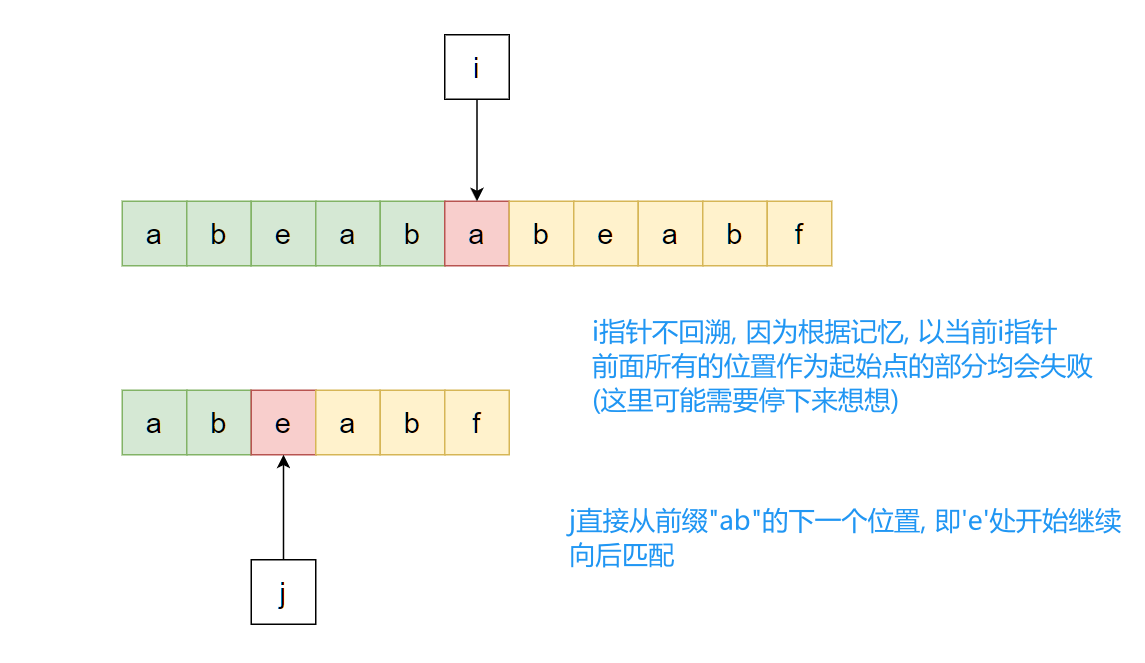
改进的思路之一为: 尝试以某种方式将之前已经扫描过的主串信息"记录"下来, 让i无需再次回溯, 换言之, i指针永不回头.

而改进的思路之二为: 在思路一中, 我们想让i无需回溯, 并且以某种方式(暂时不关心如何记录)记录下来了这种信息, 这些信息中必然包含了"主串中某些位置是和模式串的某些位置是匹配的"这一信息, 尝试提取出它们, 就可以让j指针无需每次重头开始匹配, 而是直接从一个合适的"中间位置"开始进行下一次匹配即可.

观察一个例子

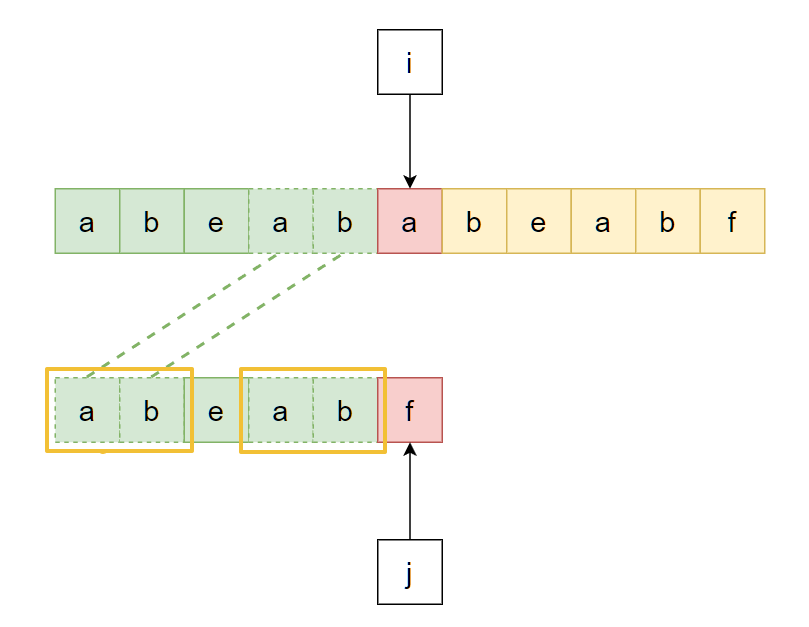
下面这个例子匹配了一部分, 此时发生了失败, 但是观察到有一些有趣的事情:
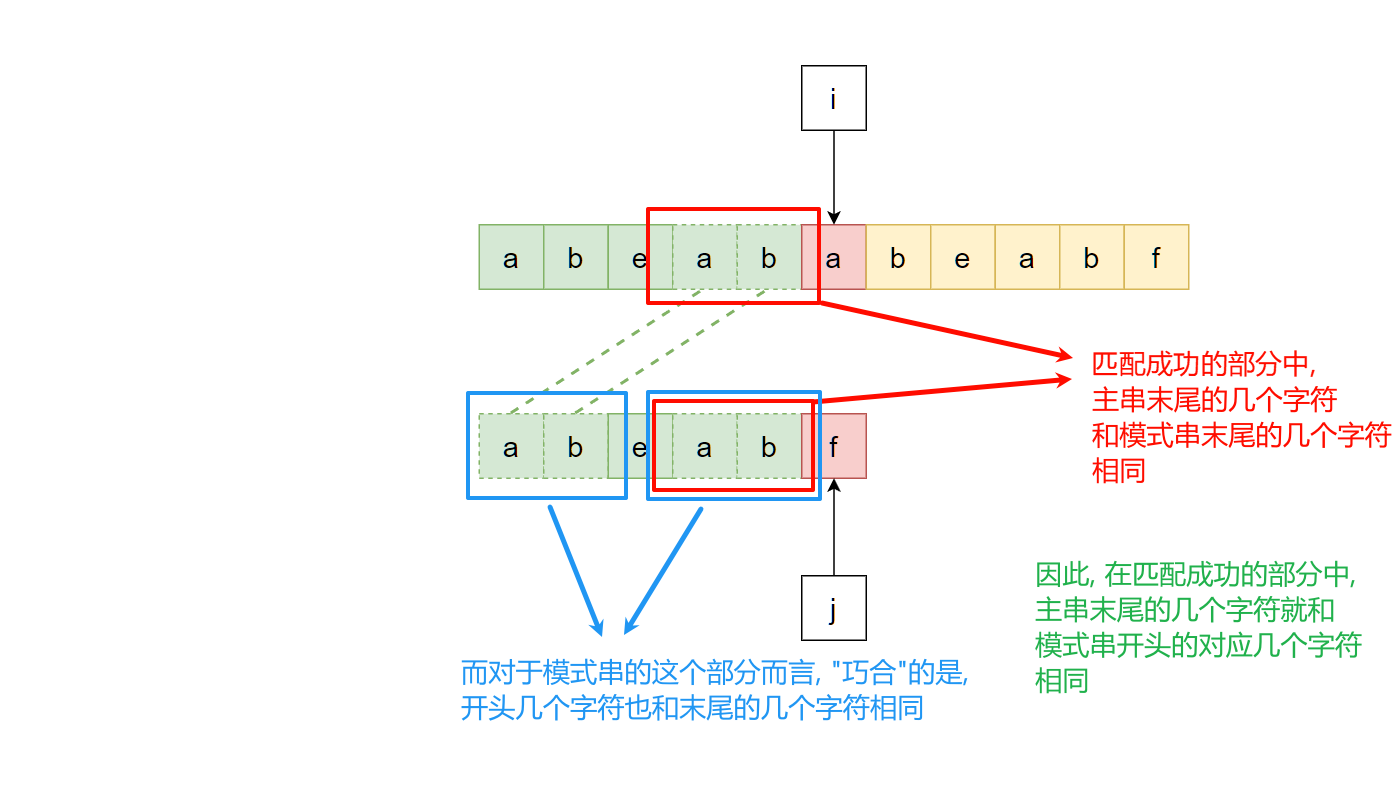
image|725
容易想到, 既然这样, 那么下一次匹配就可以直接忽略模式串中"ab"这个前缀, 直接从模式串的"e"开始继续比较即可, 也就是:
image.png|725
所以问题转化为: “从模式串当前匹配成功的部分中找到某一段前缀, 让其和主串匹配成功部分的末尾一段匹配”, 即上上图中主串和模式串开头虚线相连的"ab":
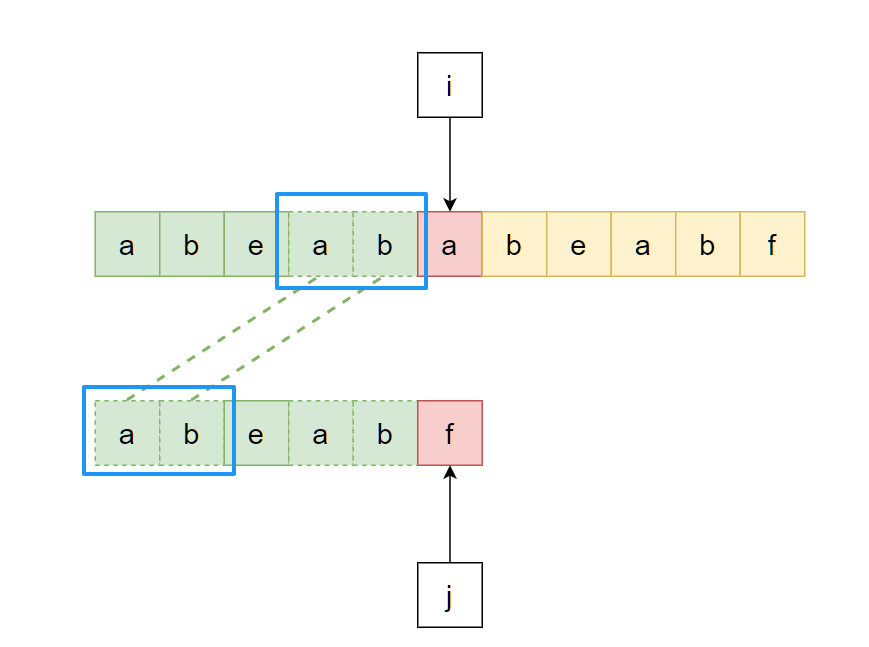
image.png|500

但是主串内容是不可控的, 并且我们期望指针i永不回溯, 因此该问题中的主串末尾那部分就需要设法以另一种方式获取到. 显然, 它就是"模式串当前匹配成功的部分中对应的后缀":
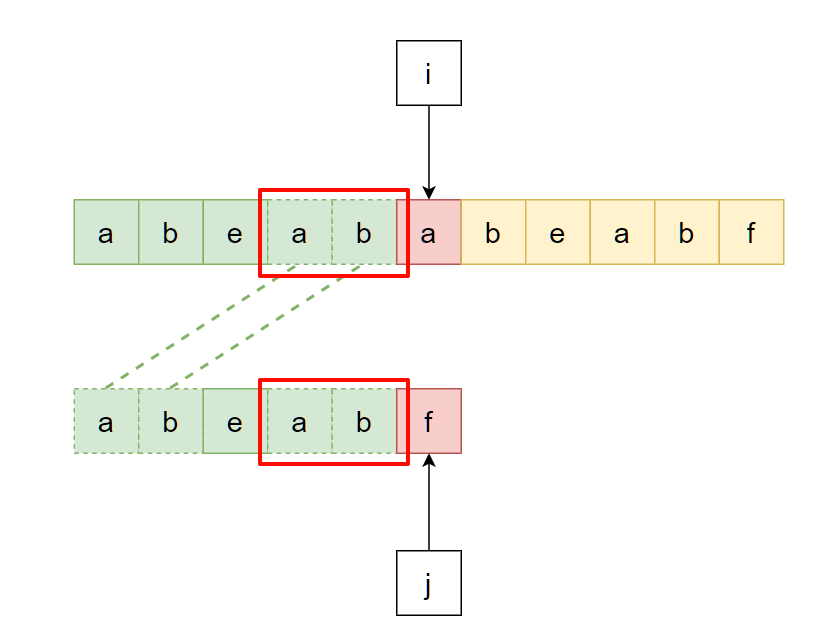
image.png|500
因此, 问题再次转化为: “找到当前模式串匹配成功的部分中, 最长的公共前后缀”:
image.png|500
之所以是"最长"的, 是因为如果所找的公共前后缀如果不是最长的, 那么就可能会跳过(忽略)主串中间本来可以正确匹配到的部分, 导致匹配失败, 这里可以自行举一个例子尝试一下.

因此, 我们问题转化为"求解一个字符串(即模式串)所有从下标0开头的子串的最长公共前后缀"

求解最长公共前后缀

我们实际的问题其实和求解最长公共前后缀有所出入, 但问题不大—我们要求的是公共前后缀中,前缀后一个字符的下标, 当然, 只要求出该公共前后缀, 求解这个下标便轻而易举.

普通解法的思路

例如上一节的例子中, 我们最终使用的就是前缀"ab"的后一个字符"e"的下标, 将j指针移动到该处.

我们使用next[]数组来存储这些值, 其中next[i]表示模式串s的子串s[0,i](包括边界)的公共前后缀中, 前缀的后一个字符的下标(其实恰好就是这个前缀的长度).

如何求解这个数组? 很容易想到, 枚举下标i, 对每一个子串s[0,i], 分别尝试以不同的前缀长度去匹配, 如果该长度的前后缀相同, 则更新. 但是这样效率极其低下.

KMP利用动态规划的思想进行递推求解next[]数组. 例如下面这个串的next数组为:
image.png|475
例如next[5]为2, 表示对应的子串"abacab"的最长公共前后缀为"ab", 其长度为2.

现在考虑如何优化. 看下面这个例子, 假设前面的next[]元素已经通过某种方式求解完成, 现在要求解最后一个元素:
image.png|475
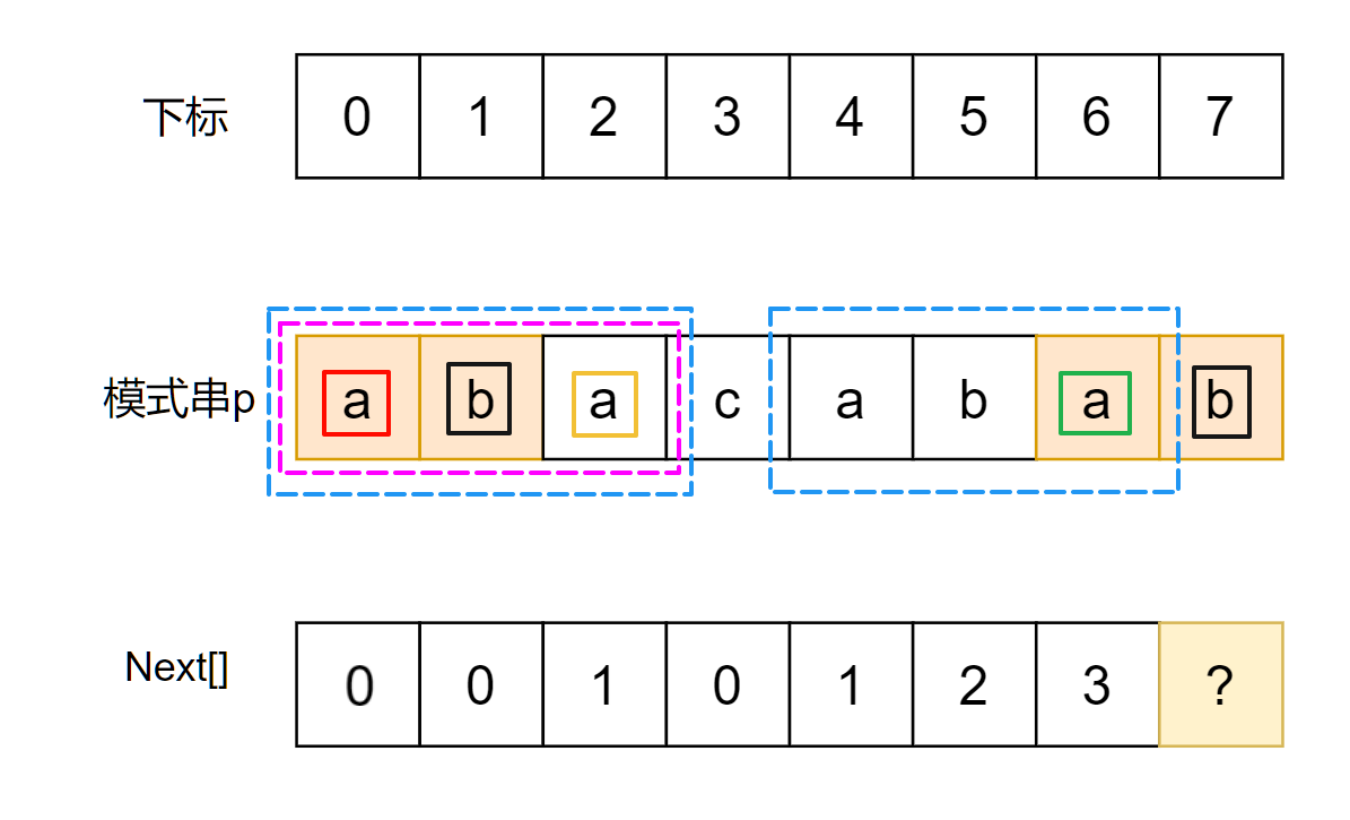
为了方便起见, 我们为图中模式串标注下标. 我们需要求解next[7], 即需要找到下图中若干红框和蓝框要相等的部分, 选出其中最长的一个:
image.png|475
不考虑优化的话, 我们大可以从大到小逐个暴力遍历这些红框和蓝框, 一一对应地检查, 直到找到一个匹配的部分, 由于是从大到小, 所以这个部分的长度就是要求的next[7]值. 结果显然是2(“ab”).

动态规划优化的思路

现在尝试优化. 先来观察一下这个"ab"所处的位置:
image.png|475
如上图, 我们可以获得如下信息:

  1. 最终的结果next[7]为黄横线所对应的2个前后缀.
  2. 根据前面的结果next[6]=3(这里假设他们通过某种方式求解得出, 这里在反推优化方式)得到, 图中2个蓝框对应的前后缀相同.
  3. 根据前面的结果next[2]=1得到, 图中2个实线绿框相同.
  4. 因为next[6]=3, 所以next[2]对应的子串"aba"(这个子串的长度对应next[6]的值)实际上就是next[6]=3对应的那个前缀部分. 根据next的定义, 图中蓝框相同, 并且实线绿框相同, 因此可以推得: 图中实线绿框和虚线绿框相同.

注：这里的next[2]就是next[next[6]-1]，减1是出于本文对next数组的定义，如果修改一下next数组的定义（见后文）则无需减1！

我们尝试根据这些信息来求解next[7](当然, 这里是从信息推结果, 反过来理解, 从结果来找出这些信息的规律也是可以的):

  1. 首先, 由于s[0,6]的最长公共前后缀为next[6]=3, 所以我们复用这个信息, 即在"aba"子串的基础上"尝试"加上后面一个字符, 分别是s[3]='c'和s[7]='b', 显然"abac"和"abab"并不相同, 匹配失败.

  2. 考虑到公共前后缀均从开头和末尾开始, 我们需要重新分配前后缀的起始位置(串的左边界), 但是发现, 无论如何, 结果一定是这样的: “找出s[0,6]中的某个公共前后缀m和n, 让前缀m加上后面一个字符, n加上后面一个字符(即s[7]='b'), 这样的相同的2个部分”.

  3. 显然, 步骤2中需要的 “s[0,6]中的某个公共前后缀m和n” 就是next[0,6]的职责所在, 而他早已被求出!

  4. 而另一个很关键的问题是, 如果步骤2匹配失败, 例如图中的蓝框, 那么我们发现图中实线绿框和虚线绿框是相同的,而实线绿框就是"next[6]=3所包含的前缀s[0,2]对应的next[2]前后缀"!

  5. 我们为其重新着色, 如下图, 原来的问题"匹配下图红框和绿框的扩展"就转移为"匹配下图红框和橙框的扩展", 当然,其中的橙框作为后缀, 其扩展是要连接上s[7]='b'而不是其后面的s[3]! (为了方便观察, 将扩展字符用黑框标识)

    image.png|475

  6. 再次回到我们的问题, 如果如步骤3所述, 在步骤2中匹配失败, 那么下一步匹配就直接去next[6]对应的前缀s[0,2]中查找. 换句话说: 我们每次比较的子串只需要更新为根据当前匹配失败的next数组元素所指向的前缀即可, 而不是像之前暴力那样仅仅递减1去缩短长度! 如果用步骤5的图来表示的话, 那就是相当于将焦点从蓝框直接转移到紫框即可.

总结一下, 上面过程最关键的一个前提就是, 使用了一个等价代换, 即将绿框等价地代换为橙框!

最终的求解流程

求解next[n]的步骤如下:

  1. 设k=next[n-1]
  2. 如果k==-1, 则查找失败, 则next[n]=0, 求解结束; 否则跳转到步骤3.
  3. 比较s[n]==s[k], 如果成立, 则next[n]=k+1, 求解结束; 否则跳转到步骤4.
  4. 更新k=next[k-1], 跳转到步骤2继续迭代.

此外需要注意的一点是, 有的实现是将next[i]定义为"模式串s的子串s[0,i-1](包括边界)的公共前后缀中, 前缀的后一个字符的下标(或称公共前后缀的长度)"
这时候需要注意一下k的初始值和更新, 不再是next[k-1], 而是next[k].
笔者在写这篇文章的时候是按照s[0,i]的定义, 后来才发现和大部分实现有出入, 不过其实无伤大雅, 只需要在求解和使用next的时候注意一下下标即可.

此外为了落实到代码, 本文的这种实现要将第一个元素设为0, 具体原因详见代码注释.

KMP简单的实现代码

使用C和Golang两种语言实现, 并附加有另一种next定义的实现(更加优雅简洁).

本文的实现方法

C语言:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <stdio.h>  
#include <string.h>  
#include <stdlib.h>  
  
#define MAX_LEN 100  
  
// 本实现的`next[i]`定义为"模式串`s`的子串`s[0,i]`(包括边界)的公共前后缀中, 前缀的后一个字符的下标(或称公共前后缀的长度)",  
// 这并不是最优雅的实现, 然而只需要简单地修改定义便可以进一步简化实现  
void get_next(char *pattern, int *next) {  
    int i = 1;  
    int j = 0;  
    next[0] = 0;  
    while (i < strlen(pattern)) {  
        if (pattern[i] == pattern[j]) {  
            next[i++] = ++j; // 之所以存储j+1的原因是，j是下标，从0开始，而next数组的每一个元素都存储的是一个实际的串（某个前缀串）的长度，因此要+1  
        } else if (j == 0) {  
            next[i++] = 0;  
        } else {  
            j = next[j - 1]; // 因为这里是next[j-1], 因此需要额外判断j是否为0, 进而本实现需要将next[0]设置为0  
        }  
    }  
}  
  
int kmp(char *text, char *pattern, int *idxs) {  
    int i = 0, j = 0, len = 0;  
    int *next = (int *) malloc(sizeof(int) * strlen(pattern));  
    size_t pattern_len = strlen(pattern);  
    get_next(pattern, next);  
  
    while (i < strlen(text)) {  
        if (text[i] == pattern[j]) {  
            i++;  
            j++;  
        } else if (j != 0) {  
            j = next[j - 1];  
        } else {  
            i++;  
        }  
  
        if (j == pattern_len) {  
            idxs[len++] = i - j;  
            j = next[j - 1]; // 注意: 这里需要回退到next[j - 1], 因为不同的匹配部分可能会重叠  
        }  
    }  
    return len;
}  
  
int main() {  
    char text[MAX_LEN];  
    char pattern[MAX_LEN];  
  
    // init  
    scanf("%s", text);  
    scanf("%s", pattern);  
  
    // search  
    int idx[MAX_LEN];  
    int len = kmp(text, pattern, idx);  
  
    // output  
    printf("index: ");  
    for (int i = 0; i < len; i++) {  
        printf("%d ", idx[i]);  
    }  
}

注：
关于该版本代码中对于KMP原理的体现问题：
当发生了前后两个字符不匹配的时候
此时j需要根据next[i-1]的值向前跳转（从原理上需要获知next[i-1]的值）
然而由于正常情况下 i 和 j同时增长，因此这个值已经隐含在j中了，因此直接j=next[j-1]即可

Golang:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
package main  
  
import "fmt"  
  
// 本实现的`next[i]`定义为"模式串`s`的子串`s[0,i]`(包括边界)的公共前后缀中, 前缀的后一个字符的下标(或称公共前后缀的长度)",  
// 这并不是最优雅的实现, 然而只需要简单地修改定义便可以进一步简化实现  
func getNext(pattern string) (next []int) {  
    i, j := 1, 0  
    next = make([]int, len(pattern))  
    next[0] = 0  
    for i < len(pattern) {  
       if pattern[i] == pattern[j] {  
          j++  
          next[i] = j  
          i++  
       } else if j == 0 {  
          next[i] = 0  
          i++  
       } else {  
          j = next[j-1] // 因为这里是next[j-1], 因此需要额外判断j是否为0, 进而本实现需要将next[0]设置为0  
       }  
    }  
    return  
}  
  
func kmp(text, pattern string) (res []int) {  
    i, j := 0, 0  
    next := getNext(pattern)  
  
    for i < len(text) {  
       if text[i] == pattern[j] {  
          i++  
          j++  
       } else if j != 0 {  
          j = next[j-1]  
       } else {  
          i++  
       }  
       if j == len(pattern) {  
          res = append(res, i-j)  
          j = next[j-1] // // 注意: 这里需要回退到next[j - 1], 因为不同的匹配部分可能会重叠  
       }  
    }  
    return  
}  
  
func main() {  
    var text, pattern string  
    _, _ = fmt.Scanln(&text)  
    _, _ = fmt.Scanln(&pattern)  
  
    idx := kmp(text, pattern)  
    for i, v := range idx {  
       if i != 0 {  
          fmt.Print(" ")  
       }  
       fmt.Print(v)  
    }  
}

优化的实现方法

该实现需要修改next[]的定义为: “模式串s的子串s[0,i-1](包括边界)的公共前后缀中, 前缀的后一个字符的下标(或称公共前后缀的长度)”

C语言:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <stdio.h>  
#include <string.h>  
#include <stdlib.h>  
  
#define MAX_LEN 100  
  
// 本实现的`next[i]`定义为"模式串`s`的子串`s[0,i-1]`(包括边界)的公共前后缀中, 前缀的后一个字符的下标(或称公共前后缀的长度)"  
void get_next(char *pattern, int *next) {  
    int i = 0;  
    int j = -1;  
    next[0] = -1;  
  
    while (i < strlen(pattern)) {  
        if (j == -1 || pattern[i] == pattern[j]) {  
            next[++i] = ++j;  
        } else {  
            j = next[j];  
        }  
    }  
}  
  
int kmp(char *text, char *pattern, int *idxs) {  
    int i = 0, j = 0, len = 0;  
    int *next = (int *) malloc(sizeof(int) * (strlen(pattern)+1)); // 注意这里数组长度要加1!  
    size_t pattern_len = strlen(pattern);  
    size_t text_len = strlen(text);  
    get_next(pattern, next);  
  
    // 注意, 由于text_len和pattern_len的类型是size_t, 因此需要使用!=而不是<  
    while (i != text_len && j != pattern_len) {  
        if (j == -1 || text[i] == pattern[j]) {  
            i++;  
            j++;  
        } else {  
            j = next[j];  
        }  
  
        if (j == pattern_len) {  
            idxs[len++] = i - j;  
            j = next[j];  
        }  
    }  
    free(next);  
    return len;  
}  
  
int main() {  
    char text[MAX_LEN];  
    char pattern[MAX_LEN];  
  
    // init  
    scanf("%s", text);  
    scanf("%s", pattern);  
  
    // search  
    int idx[MAX_LEN];  
    int len = kmp(text, pattern, idx);  
  
    // output  
    printf("index: ");  
    for (int i = 0; i < len; i++) {  
        printf("%d ", idx[i]);  
    }  
}

Golang:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
package main  
  
import "fmt"  
  
// 本实现的`next[i]`定义为"模式串`s`的子串`s[0,i-1]`(包括边界)的公共前后缀中, 前缀的后一个字符的下标(或称公共前后缀的长度)"  
func getNext(pattern string) (next []int) {  
    i, j := 0, -1  
    next = make([]int, len(pattern)+1) // 注意这里next的长度要+1  
    next[0] = -1  
    for i < len(pattern) {  
       if j == -1 || pattern[i] == pattern[j] {  
          i++  
          j++  
          next[i] = j  
       } else {  
          j = next[j]  
       }  
    }  
    return  
}  
  
func kmp(text, pattern string) (res []int) {  
    i, j := 0, 0  
    next := getNext(pattern)  
  
    // 与C的strlen不同, len()返回的是有符号整数, 因此无需使用!=  
    for i < len(text) && j < len(pattern) {  
       if j == -1 || text[i] == pattern[j] {  
          i++  
          j++  
       } else {  
          j = next[j]  
       }  
  
       if j == len(pattern) {  
          res = append(res, i-j)  
          j = next[j]  
       }  
    }  
    return  
}  
  
func main() {  
    var text, pattern string  
    _, _ = fmt.Scanln(&text)  
    _, _ = fmt.Scanln(&pattern)  
  
    idx := kmp(text, pattern)  
    for i, v := range idx {  
       if i != 0 {  
          fmt.Print(" ")  
       }  
       fmt.Print(v)  
    }  
}